Irreversible processes. Since structural global regularities are simply the continued existence of material structures in a closed or isolated region, they seem rather trivial. But structural causation can have more dramatic effects when it is combined with material causation. Since material objects coincide with space, their unchanging geometrical structures can fit together with the geometrical structures involved in the tendency toward kinetic energy and the tendency toward randomness, since the latter also coincide with space. In both tendencies, there are geometrical structures that are wiped out by how bits of matter move and interact. The inherent geometrical structure of potential energy is lost in the tendency toward kinetic energy, and the geometrical structure of non-random distributions of causally relevant factors is lost in the tendency to randomness. Material structures can channel the flow of matter through these geometrical forms, because their geometrical structures coincide with parts of the same region of space where these tendencies are exhibited. The reason that those tendencies are called “free energy” is that material structures can thereby channel the thermodynamic flow of matter from potential energy through kinetic energy to evenly distributed heat to to bring about states of those regions that would not otherwise occur. That is how machines use free energy to do mechanical work.

What makes it possible for machines to use free energy to do work can be explained ontologically, because we have already explained how material structures are ontological causes that structure the motion and interaction of other bits of matter in the region. Ordinary machines have unchanging structures that are large enough to think of them as ordinary macro-level material objects, by contrast to the micro-level objects mentioned in describing thermodynamic processes. Let us distinguish two ways that machines do work, depending on whether the free energy comes from the tendency toward kinetic energy or from the tendency toward randomness.

Free energy from the tendency toward kinetic energy. A machine has an unchanging geometrical structure as a whole that constrains how the parts of which it is composed can move and interact with one another. Potential energy also has a geometrical structure, and when the spatial relations among the forces involved combines with the unchanging structure of a material object, the tendency of potential energy to become kinetic energy can be channeled in ways that produce useful outcomes (although it often involves complex processes in which the kinetic energy is converted into other forms of potential energy and back again to kinetic energy in order to produce the kinds of changes that are desired).

This can be seen in a wide variety of cases. For example, the potential energy of gravitation can be tapped by water wheels and other structural causes, such as cog wheels, levers, wedges, and the like, to release kinetic energy in a way that grinds corn, weaves cloth, or does other mechanical work.

Free energy from the tendency toward randomness. The nonrandom distributions of efficient causes that wipe themselves out in the tendency toward randomness are made up of objects on the micro-level, but since the nonrandom distribution itself is a geometrical structure of the region as a whole, it can fit together with macro-level material structures to do mechanical work. Distributions of three kinds of efficient causes had to be mentioned in explaining the tendency to randomness (the rest masses, kinetic energies, and momentums of molecules), and we can find examples of machines using each of them.

The most familiar example involves the uneven distribution of kinetic energy. The difference in temperature between two, spatially-separated sets of material objects is what enables the steam engine to tap the free energy that exists in the flow of kinetic energy from hot to cold. The kinetic energy released by combustion of fuel flows across the wall of a box to water, producing steam at high pressure, and its expansion against a piston in a cylinder does mechanical work, such as propelling a train along a track. Internal combustion engines are as much heat engines as steam engines, although they eliminate the step in which the flow of kinetic energy conducts heat from the combustion of fuel to the water being heated by burning the fuel in the very cylinder where the piston is pushed.

The other two causally relevant factors whose uneven spatial distributions tend to wipe themselves out can also be tapped by structural causes to do work. The free expansion of a gas is used in jet propulsion, and the uniform direction of momentums contained in a wind can be caught by a sail to pull a boat along. In the latter case, it is even clearer that the free energy comes from the flow of matter through region-wide geometrical forms that is evening out the directions of momentum, for a sail can propel a boat across wind or, better yet, against it; the free energy comes, not just from going along with the wind, but from making the molecules’ directions of momentum more random. The same principle applies in wind mills and turbines.

In either case, whenever machines use free energy to do work, the geometrical structure of some material object engages with some region-wide geometrical structures involved in the tendency toward kinetic energy or the tendency toward randomness so that the thermodynamic flow of matter toward evenly distributed heat is structured to do mechanical work. The kind of work done depends on how the material structures coincide with the geometrical structure of the potential energy or the nonrandom distribution of causally relevant factors on the macro level in the region.

In some machines, both tendencies are involved. For example, the potential energy of the forces exerted at one location are communicated in hydraulic machinery by using the tendency to randomness in liquids confined in cylinders to transfer the kinetic energy and momentum from one location to another. Electrical machinery works by the same principle, except that the potential energy is communicated by freely moving electrons confined to conductors, and the work is usually done because of the magnetic forces set up by moving electric charges.

In sum, there are two kinds of global regularities caused ontologically by material structures, reversible and irreversible processes. What makes irreversible processes different is that what is being structured is a thermodynamic flow of matter (that is, motion and interaction in the region of a kind that is changing from potential energy to kinetic energy or in which a nonrandom distribution of causally relevant factors is wiping itself out). When there is no thermodynamic flow of matter toward evenly distributed heat, entropy is already maximum, and the global regularity is just a kind of geometrical structure that holds of the whole region over a period of time because some of the material objects moving and interacting there are composite objects with geometrical structures that do not change. That kind of global regularity was illustrated in the last section by the box of gas and the interlocked rings. Any change that takes place in such a region wide process could take place in the opposite direction in time. But when a thermodynamic process is going on in the region and a material structure uses its free energy to do mechanical work, the change that occurs in the region is temporally asymmetric. The work done depends on their being matter flowing through geometrical forms from potential energy to evenly distributed heat, and since some free energy is always lost to increasing entropy in the process of using it to do mechanical work, the change taking place in a closed system cannot return to its starting point.

Since reversible structural global regularities do not depend on material global regularities (except for how material structures are a byproduct of the tendency of potential energy to become kinetic), they are not included in the following diagram of the relationships among global regularities.

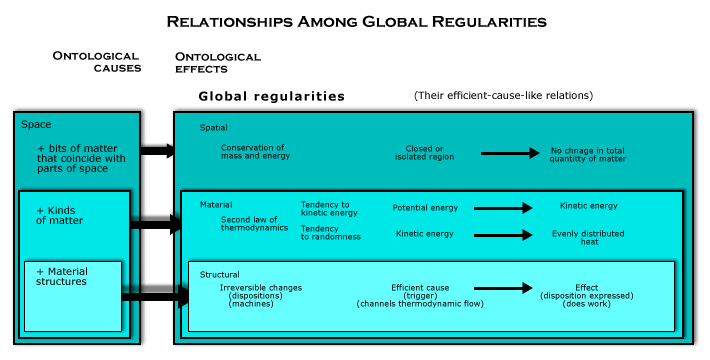
The essential role of space as an ontological cause of global regularities is confirmed by irreversible process, for it is what makes it possible to combine material and structural global regularities. This can be seen in the steam engine, the concrete phenomenon that led to the discovery of the second law of thermodynamics.

The wholeness of space plays the same role in all global regularities: it makes the motion and interaction of the bits of matter in the region add up over time. But the structure of space plays a further role in generating the material and structural global regularities, because there is a geometrical aspect to how the motion and interaction adds up as time passes. The regularity caused by material causation is that two kinds of geometrical structures about the region as a whole disappear, and the regularity caused by structural causation is that the region contains material objects whose geometrical structures do not change. In both cases, these geometrical structures are superimposed on the uniform structure of the space in the region, and that is what explains how these two global regularities can be combined, for it is simply a matter of how the thermodynamic structures fit together with the material structures.

Steam engines, for example, are just material structures combined with various thermodynamic processes in the same region of space. The free energy consumed by steam engines is kinetic energy that comes from combustion, that is, the tendency of potential energy in the fuel to become the randomized kinetic energy of heat. This kinetic energy is supplied where the material objects losing some of their rest mass are located. But since that happens in a part of steam engine, material structures can channel it to do work before the tendency to randomness evens out the nonrandom distribution of this randomized kinetic energy. It makes water in the boiler heat up, and as the spatial distribution of causally relevant factors tends to even out, and the momentum of the fast-moving molecules drives a piston in a cylinder, doing mechanical work, such as lifting a weight in a gravitational field. The way that the unchanging geometrical structures of composite material objects coincide in space with the region-wide geometrical structures that are disappearing due to the thermodynamic flow of matter toward evenly distributed heat is what explains how it is possible for heat engines to tap the free energy contained in such thermodynamic processes to do work, and that confirms the role of space an ontological cause in both kinds of global regularities.

Perpetual motion machines. These examples of machines doing work illustrate how material structures can combine with the free energy contained the thermodynamic flow of matter toward evenly distributed heat to produce changes that would not otherwise occur. But since machines can do work, it might seem that they could structure it in ways that would restore the free energy they are using. By returning kinetic energy to its potential form or imposing a new nonrandom distribution of causal factors on the dynamic process, structural causes would be doing work without entropy increasing, that is, without using up free energy. If the work done restored the geometrical structure containing the free energy it uses, it would be a machine that continues doing work forever, or a perpetual motion machine.

It is not, however, possible, because any machine that structures a thermodynamic flow of matter toward evenly distributed heat is itself part of a larger process in which such a thermodynamic flow is taking place. The machine itself is not exempt from the law of entropy increase, if only because some of the free energy becomes evenly distributed heat by flowing through the machine. The machine itself is just another part of a region where the material global regularity holds.

This can be illustrated by a pendulum swinging in a gravitational field, the example used to illustrate the tendency toward kinetic energy. The material structure constrains the motion and interactions of its parts so that the gravitational potential energy that the bob has at its maximum height is released as kinetic energy, and that kinetic energy is used to do the work of restoring it to its potential form. But it cannot go on forever, because the potential energy that is given up in each swing is never fully restored. When it is kinetic, the pendulum gives up part of its energy to other objects with which it interacts (for example, as it collides with molecules in the air and causes friction in the rope suspending it), according to the tendency of potential energy to become kinetic energy describes. And the tendency toward randomness means that the thermodynamic flow of matter through region-wide geometrical forms continues until the matter becomes kinetic energy on the micro level and winds up as heat energy evenly distributed throughout the region. Thus, the pendulum slows down and eventually stops swinging altogether.

Similarly, an elastic ball cannot bounce forever, using kinetic energy to exchange gravitational potential energy for the electromagnetic potential energy embodied in the ball’s deformation, because once the energy is released as kinetic energy, it is not fully restored.

More generally, free energy can be stored in machines, either as potential energy, kinetic energy on the macro level, or as cyclic transformations between potential and kinetic energy. But when energy is kinetic, interactions with other material objects divide up the energy until the energy is randomized on the micro level and, as heat, becomes evenly distributed throughout the region. Machines produce less free energy than they consume, because some of the thermodynamic flow of matter being channeled to do work flows directly through the machine itself toward evenly distributed heat in the region.

The ultimate randomization of kinetic energy depends, as we have seen, on three factors. The material structure itself resists the randomization of two of these factors, but there is one kind of efficient cause whose randomization it cannot resist. The unchanging structure of the composite object means that the rest masses of its parts do not become evenly distributed in the region. Moreover, since they move together as a composite object, the parts all continue to have much the same directions of momentum. But the parts can have different kinetic energies (such as vibrations within the forces holding them together), and kinetic energy does tend to become evenly distributed among them, for any inequality in the distribution of kinetic energy is a geometrical structure that tends to wipe itself out. This aspect of tendency toward randomness will continue until heat is evenly distributed throughout the region and everything has the same temperature.

There are, therefore, no perfectly efficient machines. Machines use free energy to do work, but as they do, some of it is inevitably lost as heat energy, which becomes evenly distributed in the region, increasing entropy in the region. The efficiency of a machine is measured by how much of that free energy is actually made to do mechanical work as that happens.

Examples of structural global regularities from nature. Using machines designed by humans to illustrate structured thermodynamic processes should not, however, keep us from seeing how structural ontological causes are responsible for global regularities found in nature. I will describe some of them here, because these varieties of structural causation will be used to explain how reproductive causation get started in planetary systems.

The unchanging structures of atoms are, for example, structural causes of the molecules that form naturally from them. The relevant geometrical structure of the atom is the number of electrons the nucleus can bind in the outermost shell. The ways in which the geometrical structures of the atoms and the forces exerted by their parts fit together geometrically explains why their motion and interaction add up over time in the structure of space to the formation of molecules, a composite object with a higher level of part-whole complexity. The free energy for their bonds comes from the forces exerted by their parts (the positive charges of the nuclei attracting the negative charges of the electrons), and since the potential energy released by their formation becomes kinetic energy (or radiation) that eventually becomes heat evenly distributed throughout the region, it is irreversible. The formation of molecules is, therefore, a naturally occurring irreversible structural global regularity.

In a similar way, the structures of the molecules can, in turn, be structural causes of yet higher levels of part-whole complexity. The formation of crystals involves the attachment of one molecule after another to a growing, regular geometrical structure.^[1] It is an example of structural causation, because the growth depends on how the geometrical structures of the molecules fit together with the crystal structure created by the attachment of the last molecule and how the forces exerted by corresponding parts affect one another. It is an irreversible structural global regularity, because it depends on the free energy supplied by forces exerted by their parts (often hydrogen bonds, which are weaker than those responsible for the molecules). And the result is a new kind of material structure. The kinetic energy released becomes part of the evenly distributed heat, and the bonds of the molecules making up the crystal cannot be broken without additional free energy, that is, unless enough energy is concentrated at just the right point at the right moment to free the molecule from its bonds to the crystal.

In living objects, more complex structures of molecules have more complex effects, such as the spontaneous formation of plasma membranes in water and of complexes made up of various protein molecules from their random motion and interaction. Plasma membranes are self-assembling structures used as barriers in biological processes. They are made of phospholipids, which are long, skinny molecules that tend to line up like matches alongside one another as sheets (because of weak, Van der Waals forces between them). The sheets form double layers in water (since their hydrophobic surfaces are pushed together), and the sheets tend to close on themselves in water to form spheres.

Similarly, protein molecules are amino acid molecules linked together like a chain (by peptide bonds), and the geometrical structures (or “conformations”) they take on in water often fit together in such a way that weaker forces between corresponding parts hold them together and make them stable.

Molecules have structural effects other than merely forming higher levels of part-whole complexity in material objects. They can act more like machines. For example, their structure can give them a behavior as a whole that produces another kind of material structure, which then serves a structural cause. This occurs in protein molecules, the long chains of various kinds of amino acid molecules that are the basic micro-level machines in living organisms. Such chains can bend at their chemical bonds so that weaker forces exerted by the various amino acids bind parts of the chain to one another, giving the whole chain a further geometrical structure as a whole. (That is, the unchanging structure of the protein molecule not only constrains the motions of its links relative to one another as they move in the water and determines how the chain can bend, but it also thereby determines which kinds of amino acids will be next to one another when it bends in certain ways and, so, where weaker bonds will form among the parts.) The resulting “conformation” of the protein is usually the relevant material structure that structures thermodynamic processes in living organisms. (The DNA molecule has a similar behavior as a whole: the structure of the molecule so constrains the motions of its parts relative to one another that DNA winds up as a double helix.)

Molecules can also be material structures that produce new material structures by acting on other molecules. They are called “catalysts”. But the most dramatic examples are proteins whose conformational structure makes them “enzymes”. Such proteins hold other molecules together and distort their shapes so that new chemical bonds form among their parts, replacing the old, and thereby producing molecules that are otherwise not likely to be formed at the prevailing temperature. Such molecular machines are responsible for the replication of DNA and the synthesis of proteins.

In DNA replication, proteins in conjunction with a DNA molecule are a structural cause that catalyzes a long series of chemical changes in other molecules so that another molecule acquires its structure. The geometrical structure of the DNA and protein molecules does not change, but it temporarily binds other molecules in a way that causes bonds to form in them. Each such structural effect leaves both the original DNA molecule and the copy being formed in a slightly different state, so that a different kind of molecule will interact with it the next time and the whole series results in a copy of the original sequence. In a similar way, a series of structural effects is responsible for synthesizing strands of amino acids into proteins, this time, using an RNA molecule as the template and consuming energy from other molecules in the process. But the structural cause in this case is an enormously complex object with fifty-some different kinds of proteins and several strands of RNA (together with tRNA to supply the parts).

Enzymes bring out the appropriateness of thinking of the unchanging structures of molecules as machines. The free energy for the catalyst’s work comes from the potential energy of the forces by which the enzyme binds with the other molecules (the “substrate”), but that energy is not ultimately lost to randomness, because it is paid back from the free energy released in their forming stronger bonds as the other molecules are freed from the enzyme. Thus, the enzyme can act again. Enzymes can even construct complex molecules with weaker, energy-rich bonds by extracting free energy from energy-rich molecules available in the medium.

On a larger scale, what are called “physical properties” of bulk matter, from rigidity and elasticity to transparency, color and conductivity, are dispositions to behave in certain ways under certain circumstances. But they can all be explained as irreversible structural global regularities. The conditions under which the disposition is exhibited supply a form of free energy, and the way the material structures at the micro level within the composite object structures that thermodynamic processes explains why the physical object behaves as it does under those conditions.

The simplest case is rigidity itself, in which a force exerted on part of a composite object is communicated to other parts because of the bonds that are responsible for its unchanging geometrical structure.

This is the ontological explanation of the principle of the lever. The force exerted at the end of a lever on one side of the fulcrum moves the other end of the lever through a distance that depends on the geometrical structure, and thus, if the distance the other end must move is less, a weak force operating over a longer distance becomes a strong force operating over a shorter distance. It is simply how the material structure coincides with the free energy, in this case, the force being exerted on one end of the lever.

The collisions of billiard balls are an example of how rigidity itself is a structural cause. As the first ball hits the second and comes to a stop, the kinetic energy is absorbed, but since they are elastic, the energy is stored as potential energy in the forces among the parts of the billiard balls, and as those forces restore the shapes of the balls, their potential energy becomes kinetic energy again, making the second ball move away (conserving the total momentum of their interaction). The structural cause in the billiard balls is what is unchanging about the spatial relations of their parts as they absorb and release energy.

In malleable materials, by contrast, the structural causes lie wholly in the unchanging structures of the parts, because they are the only geometrical structures that do not change when the disposition is exhibited. Energy is absorbed locally from the forces imposed, because the molecules have shapes that allow them to switch their bonds with one another, giving the parts of the composite object new spatial relations to one another as parts of the whole. That is how the motion and interaction of the material structures add up in space, when they start out with such bonds to one another and free energy is supplied by a force being impressed.

Material objects also have other mass properties that can be explained in similar ways, such as transparency, electrical conductivity, heat conductivity. The colors that material objects appear to have when illuminated by the whole spectrum of visible photons comes from some wavelengths being absorbed, while others are reflected. The material structure responsible for this global regularity lies in various aspects of the micro-structure, which interact differently with different wavelengths of light. (But colors in this sense are, of course, physical properties, and they must be distinguished from the appearances of colors to the subject, which are qualia.)

The explanation of dispositions by material and structural ontological causation is a reduction of those regularities to spatiomaterialism, and since that demonstrates their (conditional) ontological necessity, it explains the nature of the casual connection involved in these efficient causes. In the case of dispositions, the regularities connecting causes and effects are just irreversible structural global regularities, whose ontological causes are like machines built into nature. The test conditions of the dispositions are the efficient causes, and what happens are the effects.