Material Global Regularities. The second law of thermodynamics, like the first, is stated as a regularity about the change in a total quantity that holds of closed region of space: the total entropy cannot decrease, though it may increase and usually does until it is maximum. It is also possible to explain the second law of thermodynamics ontologically, given that matter obeys the basic laws of physics. Once again, it an ontological effect that space has on the world because space, like matter, is a substance enduring through time and it contains all the bits of matter. Unlike the explanation of the conservation of matter, however, the explanation of the law of entropy depends not only on the principle of local motion, but also on matter having the more specific nature described by the laws of physics, whose truth was explained in Contingent laws. The reason is that there are geometrical aspects about the various forms of matter involved, and thus, not only does the wholeness of space require that all their local changes add up over time, but the structure of space requires the motion and interaction of the bits of matter to add up in a certain way geometrically.

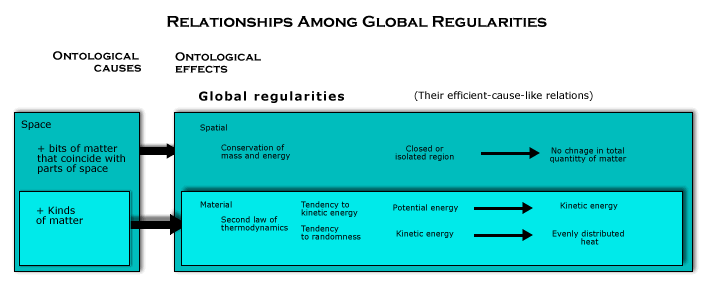
The first and second laws of thermodynamics. The spatial and material global regularities made their appearance in physics as the first and second laws of thermodynamics. These laws were originally formulated to describe certain phenomena that were discovered in the development of steam engines. Physicists knew that steam engines could extract mechanical work from heat energy, but when they recognized that the total energy in a closed system does not change (the first law of thermodynamics), they had to admit that only some of the energy in such a system could be used to do mechanical work, for a closed system could change in ways that make it unable to do work. They knew that what makes it possible to extract mechanical work from the energy contained in such a system is a flow of heat from high temperature regions to regions with a lower temperature. The energy that is available to do work was called “free energy” (or “usable mechanical energy”). Thus, they recognized that, although the total energy in a closed system does not change, the free energy does. The free energy can decline and usually does. A quantity was introduced as a measure of the portion of the total energy in the system that could not be used to do mechanical work. They called it “entropy”. Thus, in these terms, the second law of thermodynamics holds that the entropy in any closed system never decreases. It may increase, and usually does, stopping only when it becomes maximum. But it never decreases. What decreases as entropy increases is free energy. The notion that there is a form of energy that declines, even though energy is conserved, was puzzling. And though it was discovered by thinking about steam engines, the second law of thermodynamics was eventually recognized to hold for systems of all kinds. The law of entropy increase is universally true, holding everywhere (except possibly for the origin of the universe in a big bang or the alternative to the big bang to be proposed in Cosmology).

The free energy available in a system has something to do with “order”, but it has never been very clear what order is in general or how it makes energy free.^[1] In the case of steam engines and heat engines generally it is clear what the relevant order is. It comes down to the temperature differences between parts of a system and the quantities of heat each contains, for the flow of heat between them is what makes it possible to extract mechanical energy. But when the law of entropy is generalized to cover systems of all kinds, it is less clear what the nature of the order is.

It is, however, possible to explain order of all kinds in an intuitively clear way, if we take the wholeness of space into account as an ontological cause of global regularities, along with matter as contained by space. Energy is, in our terms, a form of matter, the same stuff that accounts for the rest mass of material objects, though there are several, basically different forms of energy—kinetic energy and the energy due to forces, both potential and actual (especially, photons). What makes energy free is, as we shall see, a geometrical aspect of these forms of matter and how they are contained in a region of space, for there are regularities about how such geometrical properties change over time. Showing that these global regularities follow from spatiomaterialism is, therefore, an ontological explanation of why the first and second laws of thermodynamics are true. It will require not only the material global regularities, but also the structural global regularities (to be discussed next). However, not only will that prove their ontological necessity, but it will also make clear what these regularities are all about in their full generality, including the way in which free energy depends on order.

Two global regularities are involved in making the second law of thermodynamics true according to this ontological explanation. The first is the tendency of potential energy to become kinetic energy or photons (or the tendency toward kinetic energy), and the other is the tendency of dynamic processes to become random (or the tendency toward randomness). Both are ways in which the specific nature of matter works together with space as an ontological cause to constitute a global regularity. But they work together, because the first is usually the source of the situations in which the second global regularity is exhibited. Let us consider each in turn and then see how they are combined.

The tendency toward kinetic energy. The first global regularity included in the second law of thermodynamics is the tendency of potential energy to become kinetic energy (and photons). The very name, “potential” energy, suggests this tendency, because potential energy is actualized by becoming kinetic energy (and/or photons). Though it is also possible for kinetic energy to become potential energy, the tendency is toward kinetic energy, because potential energy that has become actualized is less likely to restore itself. In order to see why, we need only contrast the natures of potential energy and kinetic energy. The same kind of contrast also shows that potential energy tends to be lost to other kinds of energy, such as photons, but to keep it simple, let us focus on kinetic energy for now.

When potential energy becomes kinetic energy, the kinetic energy comes from the forces that material objects exert on one another. According to our ontological explanation of the basic laws of physics, potential energy is actually a form of matter that constitutes the force fields themselves (and whose quantity is already counted in the rest masses of the objects exerting the forces). A force is called a field because its (potential) effects are distributed in the space around the object imposing the force, with a geometrical structure centered on the location of the object. That force field is explained ontologically by a form of matter that coincides with all those parts of space at once, and thus, the matter has a geometrical structure. The matter making up the force is spread out continuously in space, varying with the strength of the force it exerts. That geometrical structure means that there is a wholeness about the energy when is still potential, because each part contributes to the total potential energy (and, thus, to the total rest mass of the material object exerting the force) by having a definite location relative to every other part.

Kinetic energy, by contrast, is a form of matter that is not only attached to the material object, but also located at its center of mass. Kinetic matter, as we are calling it, has a location that enables it to connect the material object to space in a way that makes the object move across space in some direction at a certain speed. But that means that kinetic energy (or kinetic matter) lacks any inherent geometrical structure, except for the location of the object and its direction in the region where it exists.

Given that potential energy has an inherent geometrical structure and that kinetic energy does not, we can see why there is a tendency of potential energy to become kinetic energy in the motion and interaction of material objects by considering what is involved in the conversion between them. In order to convert potential energy into kinetic energy, more than one material object must be involved, because kinetic energy is actualized as material objects are accelerated by the forces they exert on one another. Such acceleration can occur only when the objects are spatially related so that the forces they exert on one another are able to accelerate them, and when they are a source of much energy, they are rather special. Objects at rest, for example, can acquire kinetic energy from attractive forces only when they are separated by a distance that can be closed by their acceleration (and they can acquire kinetic energy from repulsive forces only when they are located near one another and can move away). When objects are accelerated, however, the objects change their locations in space, and that changes the capacity of the force to accelerate them, because it decreases the special kind of spatial relationship needed to accelerate them. The potential energy has been consumed, and in its place the objects have some kinetic energy. The kinetic energy actually comes from the matter constituting the force field, and that is possible because the force field itself has changed in a way that requires less matter to constitute it. Thus, what has happened is that some of the matter that had an inherent geometrical structure has been extracted and has become matter that is located with the objects’ centers of mass. The matter’s loss of inherent geometrical structure is what is responsible for the temporally asymmetric tendency, for that makes it a form of matter that can be divided up among many other material objects as they interact. In particular, according to Newton’s laws of motion, when an object with high kinetic energy interacts slower moving objects, some of its kinetic energy is carried away by the other objects, being divided up among them.. It is not very likely that other objects will ever move in just the right ways to restore the special spatial relation that accelerated the object in the first place.

For example, if an object falls toward a planet because of the gravitational forces they exert on one another, it loses its potential energy as it approaches the planet and it gains kinetic energy. But as it collides with other material objects, either on its way down or when it runs into the earth, it gives up kinetic energy, and though it may rebound, much of its kinetic energy will be lost to other objects (and to overcoming the forces that may be involved in its fragmentation or deformation). The system will never restore the object’s potential energy.

To be sure, the conversion can work the opposite way. When objects exerting forces on one another have accelerated one another and lost potential energy, they have also acquired kinetic energy, and that can restore potential energy. Objects with kinetic energy restore potential energy when their retreat from one another is slowed by attractive forces (and when their approach to one another is slowed by repulsive forces). Indeed, a system involving only two material objects may simply go on converting energy between kinetic and potential forms indefinitely, such as a planet in an elliptical orbit around its star.

The reason there is a tendency toward kinetic energy is that other material objects are usually involved. According to Newton’s laws of motion, when objects with kinetic energy interact with one another, they exchange kinetic energy in a way that tends to equalize the kinetic energy among them. Thus, objects with unusually large amounts of kinetic energy see their kinetic energy divided up into smaller bits of kinetic energy that subsequently move around separately from one another. Kinetic energy is no longer moving objects in the right locations in the right directions at the right times to restore the unusually large potential energy from which it derived.

For example, even in a pendulum, which continually converts potential energy to kinetic energy and back again as it rises and falls in the gravitational field, this tendency to kinetic energy cannot be avoided. The bob also loses kinetic energy as it collides with particles of air and as it stretches and relaxes its tether, and it never restores all the potential energy and eventually comes to a stop.

There are, of course, processes in which kinetic energy and potential energy are continually being converted into one another, such as those involved in elastic collisions or a plasma of charged particles, but the potential energy in those processes is not a source of free energy, but just part of a random interaction that is the subject of the other global regularity, as we shall see.

The wholeness of the space containing the objects and their two forms of energy is what requires all the motion and interaction of bits of matter in the region to add up over time. That is how space causes all the global regularities. But in the case of the tendency to kinetic energy, space plays an additional role, which depends on its geometrical structure. There is a geometrical structure inherent in potential energy, and since it is superimposed on the uniform structure of space, there is a geometrical aspect to how the motion and interaction of the material objects adds up over time. A region with a large amount of potential energy must have a rather special geometrical structure, because potential energy exists in the forces that objects exert and it can be converted to kinetic energy only when objects have kinds of relative locations in the force fields they impose that can accelerate them. There is a tendency to kinetic energy, because when it becomes kinetic energy, is a form of matter that is located with the center of the material object’s rest mass, thereby losing that kind of its geometrical structure inherent in potential energy. It moves across space with the material object and can be transferred to other objects by collisions, which tends, as we shall see, toward randomness. Thus, the geometrical structure inherent in potential energy tends to be erased from the region.

In other words, when potential energy becomes kinetic, matter that did exist as part of the whole force field surrounding the material objects comes to be kinetic matter located with their centers of mass, and that makes it possible for the matter to be divided up further by collisions with other material objects. Once the matter is divided up, it is unlikely that the objects will have just the right speeds in the right directions at just the right locations and just the right times to put the objects back in the same spatial relation that gave them potential energy in the first place. Indeed, it is unlikely they will put any object in any similar significant source of potential energy, for that would require assembling separate bits of matter as a form of matter (a force being exerted) whose inherent geometrical structure is testimony to its unity as a single bit of matter.

The examples used here are based on gravitation,^[2] but it should be noted that the same holds for electromagnetism and short range forces. When protons are combined randomly with electrons, their long-range attractive forces bind them together as hydrogen atoms, and though the potential energy may take the form of photons, instead of or as well as kinetic energy, the photons also lose their energy as they are scattered by other objects with electric charges and the geometrical structure inherent in potential energy is still broken up into many smaller bits.

Much the same happens in the case of short-range forces, though the spatial relations required to actualize potential energy are different. In nuclear fusion reactions, for example, nuclei must collide with enough energy to overcome an initial repulsion by the strong force, for otherwise the short-range attractive force does not reach far enough to bind them together.

Likewise, atoms (or groups of atoms) that exert attractive forces on one another may be separated too far by the molecular structures of which they are parts for their forces binds them together, until the local temperature is high enough for collisions to put them momentarily within the effective range. This is what happens when a match is used to start combustion.

Likewise in fission reactions, the potential energy of repulsion between clusters of positive charges in a heavy nucleus becomes kinetic when they fly apart, but first the nucleus must be made unstable by the absorption of a neutron.

In these cases the geometrical structure inherent in potential energy is more internal to the material objects, but that structure is still part of the geometrical structure of matter in the region, for there must be conditions in the region that will release it.

The tendency toward randomness. What tends to become random is the motion and interaction of bits of matter in a closed or isolated region, or what may also be called “dynamic processes.” In the dynamic processes used to think about this phenomenon, material objects are assumed to have repulsive forces by which elastic collisions keep them from occupying the same places at the same time.

In elastic collisions, material objects keep moving and interacting, because no kinetic energy is lost or absorbed by their parts when they interact. Force fields and conversions to potential energy are actually involved in these interactions, but they can be ignored here, because there is no net change and we want to consider what happens to their  kinetic energy and other properties of the kinetic matter attached to material objects.

The traditional model for the tendency to randomness is the motion and collisions of billiard balls in a box. Once again, it is being contained by space that requires their motion and interaction to add up over time, and all that is needed to see why there is a tendency to randomness is to consider how motion and interaction in accordance with Newton’s laws of motion add up in space over time. There is, once again, a geometrical structure about the region that gets wiped out.

In a spatiomaterial world, everything happens by the motion and interaction of bits of matter, and in this case, it is extremely simple, because the bits of matter are all material objects with rest mass and kinetic energy (that is, the kinetic matter attached to material objects). There is no geometrical structure about the material objects in the region except their locations, speeds and direction of motion. These three properties are the initial conditions that would have to be described along with Newton’s laws of nature, according to the D-N model of explanation, in order to predict and explain what happens. They are all part of the efficient cause that determines what happens in the region. But it is not necessary, or even relevant, to derive mathematically what happens in detail in particular cases. If we consider the material objects relative to the space that contains them, we can see why their motion and interaction becomes randomized before long, if they aren’t already, because it is due to a geometrical aspect that we can understand, when we see them against the background of space.

The wholeness of space is what requires the motion and interaction of the bits of matter located in the region to add up as time passes, but the structure of the space within the region is what determines how the local changes add up. The objects have locations, speeds and directions at any moment that determine a geometrical structure relative to space, and when they move and interact according to Newton’s laws of motion, local changes add up in space over time in a way that erases that geometrical structure by evening out the spatial distribution of all three of the kinds of efficient causes that are relevant.

This tendency can be seen in each of the kinds of relevant efficient causes. That is, (1) the rest masses of material objects become spread out evenly throughout the region of space, (2) their kinetic energies become evenly distributed in space, and (3) their directions of momentum also tend toward an even spatial distribution.

(1)   If there are more material objects moving and interacting in one part of the region of space than in another, as when a gas of molecules is released in a vacuum, they will spread themselves out, because, other things being equal, objects at any boundary between highly and lowly populated regions are more likely to be turned back by collisions on one side than on the other. Hence, material objects will tend to move toward the less populated region until they are all evenly distributed in space.

(The diffusion of the molecules of one gas or liquid that is released into another works similarly, because when the objects colliding have different rest masses, the directions of the motion of less massive objects tend to change more, until the more massive objects are evenly distributed among them.

(2) Randomness may still not prevail, however, when rest masses are evenly distributed in space, because objects in some areas may be moving faster than those in other areas, for example, when there are hot spots or cold spots in the region. However, such spatial unevenness in their kinetic energy is also evened out, because elastic collisions of slow-moving with fast-moving rest masses tend to speed up the former and slow down the latter. That is the only what that both kinetic energy and momentum can be conserved. Kinetic energy tends to be divided up among the colliding objects. Thus, at the boundary between regions of different temperature, symmetrical elastic collisions will be so located and oriented in space that kinetic energy is communicated to the less energetic regions (that is, by conduction of heat).

(3) Motion and interaction may still not be random, even when rest masses and their kinetic energies are distributed evenly in space, because their speeds may be mostly in the same direction, as in a wind. But any such unevenness in the distribution of direction of motion among the objects also tends to be evened out, because when kinetic energies are evenly distributed within and outside the wind (their temperatures are the same), the wind tends to be invaded by objects moving perpendicularly to it. Objects making up the wind have more of their kinetic energy tied up in moving in the direction of the wind than objects outside the wind, and thus, objects approaching the wind perpendicularly are less likely to be turned back by collisions than those traveling in other directions (that is, the pressure exerted sideways by molecules of the wind will be less than elsewhere in the region, called the Bernoulli effect). As molecules invade the wind, they collide with molecules making up the wind, which tends to make their directions more perpendicular to the wind, and such reactions are more likely until the directions of momentum of all the objects in the region are evenly distributed.

The result is that the rest masses of the objects, their kinetic energies, and their directions of motion all tend to become evenly distributed in the region. That is the tendency toward randomness, and this distribution can be described statistically. But since heat is just the kinetic energy of the molecules in these simple cases, it is a tendency of kinetic energy to become evenly distributed heat, equalizing the temperature everywhere.

This tendency continues to hold when we take various complications into account. For example, collisions among real molecules are not necessarily elastic, because they can absorb some of the kinetic energy being exchanged. But as the kinetic energy is evened out among the objects, so is the energy absorbed by their parts.

And though material objects also emit and absorb photons, the spatial distributions of the locations, directions, and energies of the photons in the region also tends to be evened out by their interactions with the material objects, assuming that photons are reflected back and the region is closed. There are no kinds of interactions that can prevent the randomness.

The tendency toward randomness is that aspect of the law of entropy that is described as heat flowing from regions of high temperature to regions lower temperature, like water from high altitudes to lower altitudes. And since kinetic energy is a form of matter, according to this ontological explanation, it can even seen as vindicating the belief that heat is a “caloric fluid” that exists in addition to the rest masses of the objects involved. It is a form of matter that flows from hot regions to cold.

There is nothing very original about this explanation of the tendency to randomness. These effects are obvious to anyone who thinks about concrete examples of this tendency. What is new is recognizing that the tendency depends not only on the nature of matter (that is, the basic laws of physics), but also on the nature of the space with parts of which all the bits of matter coincide.

Our ontological foundation entitles us to take space into account as an ontological cause in explaining regularities about change. The wholeness of space is what requires the motion and interaction of all the objects to add up over time, as in all global regularities. But how they add up over time also depends on the structure of space, for it is only against the background of space that the causally relevant factors determine a geometrical structure.

It is the lack of evenness in the spatial distribution of one or more of the relevant efficient causes (their locations, kinetic energies, or directions of momentum) that makes the state non-random. And in each case, a geometrical structure about the non-random state is what causes the tendency toward randomness. It is the structure of space that determines where their motions will lead them and which objects they will interact with next. And we have seen how the unevenness in the distribution of the causally relevant factors puts certain objects are in asymmetrical situations which will eventually even out the spatial distribution of these factors. Thus, the temporal asymmetry of the second law of thermodynamics is a result, not only of the basic laws of physics, but also of how the motion and elastic collisions of material objects obeying those laws add up over time because they are contained by space.

Thus, when we take space into account, there is no mystery about why there is a temporal direction to change in which the kinetic energy of objects in non-random states winds up as heat evenly distributed in the region. The geometrical structure involved in any unevenness about the distribution of the three relevant factors is what causes those aspects of matter to become evened out in space, that is, more like the structure of space containing them.

The second law of thermodynamics. This ontological explanation of the second law of thermodynamics reveals that two different global regularities are involved: a tendency of potential energy to become kinetic energy (and/or photons) and a tendency of kinetic energy (and/or photons) to become evenly distributed heat. In both cases, there is a geometrical structure about the region that tends to be wiped out by how objects move and interact. One is the geometrical structure that the region has because it contains the geometrical structures inherent in the potential energy of forces (which can become kinetic energy). The other is the nonrandom distribution of causally relevant factors in the region (which tends toward the randomness of evenly distributed heat). Both kinds of geometrical structures tend to go out of existence, as we have seen, because that is how the motion and interaction of the bits of matter adds up over time because of the uniform structure of the space containing them. In one case, when the energy of position becomes energy of motion, matter with an inherent geometrical structure is replaced by a form of matter that can be broken up into different pieces. And in the other case, when any of the causally relevant factors is unevenly distributed, that is a geometrical structure in the region that tends to wipe itself out over time, with kinetic energy winding up as heat evenly distributed in the region. When geometrical structures of either kind go out of existence, only very special situations can bring them back into existence. And these two tendencies are connected, because the tendency to kinetic energy supplies nonrandom dynamic processes that tend to become random. Together, they make up a temporally asymmetrical change in the region as a whole.

Given how both global regularities involve the disappearance of a special kind of geometrical structure in the region as time passes, it may be useful to suggest that the law of entropy increase can be seen as a kind of four dimensional geometrical structure in the region as a whole. In its most complete expression, the geometrical structure inherent in potential energy becomes the geometrical structure inherent in nonrandom distributions of causally relevant factors, which in turn becomes the lack of any salient geometrical structure inherent in the randomness of evenly distributed heat. At the later edge of this four dimensional structure, the bits of matter have the kind of geometrical structure that is most like the structure of the space containing it. It is as if matter in the region were coming to mirror the uniform structure of space.

This explanation of the second law of thermodynamics solves a puzzle about the reduction of the second law of thermodynamics to physics. The law of entropy seems to resist reduction to the laws of physics, because it describes a regularity about change that is asymmetrical in time, whereas the laws of physics describing how the material objects interact are all time-symmetrical. The temporal asymmetry of the law of entropy comes, however, not from the laws of physics by themselves, but from the forms of matter they describe having geometrical aspects that are casually relevant in how local changes adds up in space over time. Both tendencies involved in the explanation of the law of entropy are a result of how geometrical structures about the matter involved are efficient cause of their own extinction. That solves the problem. (See Change: Epistemological philosophy of causation: Second law of thermodynamics.)

The thermodynamic flow of matter. If we look at the second law of thermodynamics in terms of matter, the two tendencies can also be seen as a “thermodynamic flow of matter” from potential energy to evenly distributed heat. This is a flow of matter in a certain “direction” through a series of forms of matter. The matter starts off as part of the rest masses of the material objects involved, for matter in that form is what constitutes the forces that the objects exert on one another. When the objects have spatial relations in which their forces can accelerate one another, it is potential energy. And when potential energy is actualized, the matter takes the form of kinetic matter, which lacks any inherent geometrical structure, since it is a form matter that is located at the material object’s center of mass. And since interactions among material objects tend to equalize their kinetic energy (and other causally relevant factors), kinetic matter tends to become randomized as heat and evenly distributed in space as heat. Since matter flows through these forms in only one direction, however, matter winds up as evenly distributed heat, that is, with higher entropy in the region.

This thermodynamic flow can also involve potential energy becoming photons, but they are merely another route to evenly distributed heat. The photons interact with the material objects and become randomized for much the same reasons.

This is to characterize the global regularities described by the second law of thermodynamics as if the processes followed a direct path to evenly distributed heat of increasing entropy. But the thermodynamic flow of matter may include twists and turns in which some of the kinetic energy becomes potential energy in other forms only to be released again as kinetic energy before finally turning into heat that is then evenly distributed in space. As we shall see, such transformations between potential and kinetic energy are how machines use this kind of matter, as free energy, to do work. Similarly, though nonrandom distributions of the three causally relevant factors becomes evenly distributed heat, it may be used as free energy to do work, as in heat engines, which may create potential energy and give some objects high kinetic energy, before it becomes evenly distributed heat. These complications will be considered when we take up structural causation.

The transformation of free energy into entropy. To sum this up in more familiar terms, at the most general level, according to the second law of thermodynamics, what is happening in any closed or isolated region of space is the transformation of free energy into entropy. Free energy is all the energy in the region that has not yet become evenly distributed heat, where heat is simply randomness in the motion and interaction of the simplest physical objects that can move relative to one another. And entropy is, technically, a measure of how much of the total energy in the region exists in the form of evenly distributed heat. The second law of thermodynamics, or law of entropy, holds that in a closed or isolated system, entropy can increase, but it cannot decrease. That is, all the other physical forms of energy (that is, forms of matter) are ineluctably becoming evenly distributed heat.

This is the supposedly bleak image of a world made up of matter in motion which sees the universe as condemned to a “heat death.” This image has traditionally been used to discredit materialism, or at least discourage belief in it. But if we consider what it means more concretely at the scale of planetary systems, the transformation of free energy into entropy is, as we shall see, the fountain of everything valuable in the world. Free energy is what makes it possible for structural causes to do work, as we shall see next.

To talk of “free energy” is to classify energy by its capacity to be used by machines to do work, but concretely, such free energy takes many different physical forms. On the scale of a planetary system, the richest and most constant source of free energy is the star, because such a huge accumulation of mass has a gravitational field that contains an enormous amount of potential energy. The energy stored in its force field is the source of all the free energy that will eventually become evenly distributed heat (except for energy from radioactive decay). Its gravitational field constantly accelerates bits of matter toward its center. Even inside the star itself, the inward acceleration of more distant matter causes a pressure that is balanced against the kinetic energy (and photons) constituting the random motion and interaction of more centrally located particles and their electromagnetic interactions. Indeed, the kinetic energy is great enough for the collisions of protons, neutrons and small nuclei to bring them within the short range of the strong attractive force that they can exert on one another, and as it fuses them together, the potential energy of the strong force is actualized as kinetic energy and photons, decreasing their rest masses. High energy photons (and other particles) escaping at the surface of a star radiate outward toward cold, empty space, showing the surrounding planets. Since radiation is a form of free energy (like kinetic energy before it is randomized), it can be used to do work on the planets intercepting it. Not only do photons heat the planet, but they supply energy in a form that can drive chemical interactions. There is also heat from the tidal forces that planets orbiting a star suffer as they rotate on their own axis (and from the radioactive decay of particles making up the planets). The energy eventually flows through the planets, since planets also lose heat as they radiate energy into cold empty space in the form of lower-energy photons.

The star’s radiation is, therefore, a form of energy that can be used by machines on planets to do work, or free energy. This is the setting, as we shall see, for reproductive causation to generate its spectacular global regularity. But first we must consider how this thermodynamic flow can be used to do work, and that is an effect of structural causation.